 Helbring Schültz: Publikationen
Helbring Schültz: Publikationen Mathematisch- naturwissenschaftliche Texte/
Mathematisch- naturwissenschaftliche Texte/Scientific Articles
- Stellenwertsystem
- Place Systems [English]
- Ist 0-Fakultät wirklich 1?
- Is 0-Faculty Really 1? [English]
Bibelstudium/
Bible Studies
Entdeckung/
Discovery
Echte und unechte Kuriositäten/
Real and Fake Curiosities
Denkaufgaben/
Brain Teasers
Kontakt/
Contact

[Download File as a Word-Document]
Is 0! (read: "zero faculty") really 1?
Reference-books describe the mathematical function "n-faculty" e.g., as quoted by Meyers Großem Rechen Duden in the following:
"Faculty, n! (read: "n-faculty").
The product of the n numbers is called "n-faculty" for positive integer numbers. It is written n!=1 2 3 ... (n-1).
0! =1 is defined for n=0.
Example: 1! =1=1 3!=1 2 3 = 6
2! =1 2 =2 .....................
n! = nn*e-n*sqrt(2*Pi*n) can be used approximately for big numbers (Stirling formula).
0!=1 is a convention without mathematical proof and thus is not conclusively a right statement.
Following consideration makes the result 0 for 0! probable:
In the equation
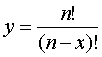
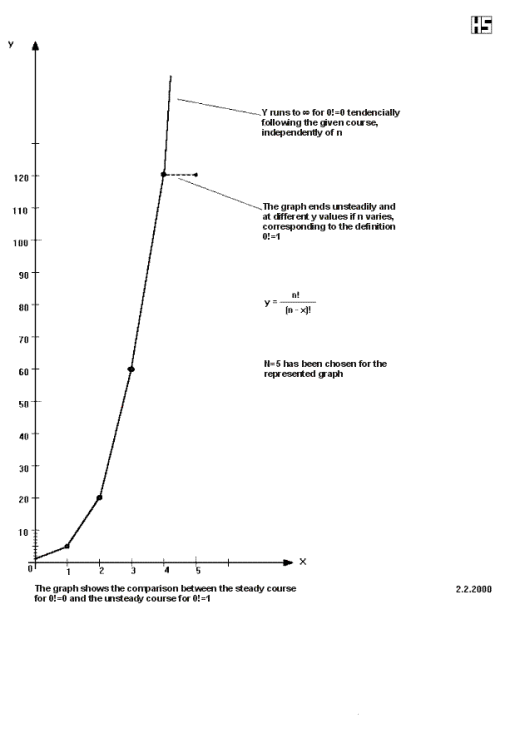
x runs from 0 to n. Then a graph y over x is created with the gained value pairs. This graph shows at x=n an unsteadiness according to the up to now existing definition for 0!=1. On the other hand a continuous course would be guaranteed for 0!=0.
Example for n=5 and x = 0,1,... 5
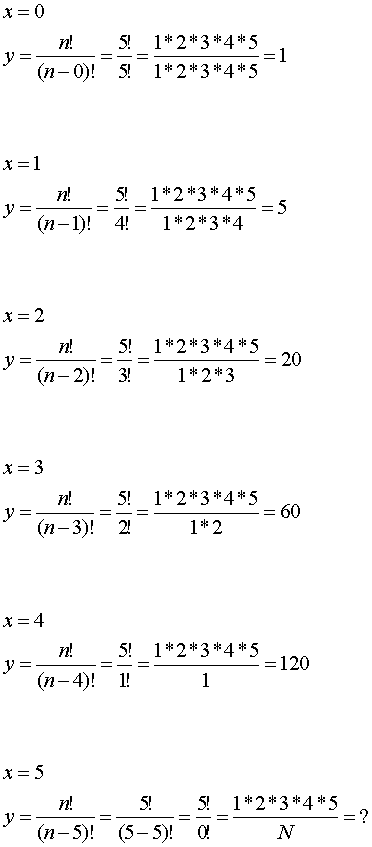
N is set for 0!=1 in the denominator according to the valid definition. From this the same value 120 for y follows for the places x=4 and x=5, and causes in the further course of the graph an unsteadiness. This is shown by the dashed line. But if N is 0!=0 in the denominator, then the graph strives to §§§ in y direction, so that the given course of the graph is continued in the right direction. See graph.
This behavior can definitely be reproduced for any number of n, e.g. n=8 with the place of unsteadiness at y=40.320, or for n=10 with the place of unsteadiness at y=3.628.800, and so on.
Because of this consideration the statement 0!=0 may be more probable then the up to now definition of 0!=1. Thus the right answer of the question asked in the headline could be: 0!=1. Beyond it the definite result of the article above can be valued as true that 0!=0.